（以下はScilab 5.5.2を元に記載しています。）

電気抵抗と同じように，比熱のシミュレーションを行ってみたいと思います。格子振動による比熱はアインシュタインの式とデバイの式があります。

アインシュタイン比熱
$$C_V(T) = 3N_Ak_B\left(\frac{\Theta_E}{T}\right)^2\frac{e^{\Theta_E/T}}{(e^{\Theta_E/T}-1)^2}$$

デバイ比熱
$$C_V(T) = 9N_Ak_B\left( \frac{T}{\Theta_D} \right)^3 \int_{0}^{\Theta_D/T}\frac{x^4 e^x}{(e^x-1)^2}dx$$

特性温度をそれぞれ300Kとして，比熱の温度変化を計算したのが下記のスクリプトです。

//------------------------------------------------------------------------//
//---    アインシュタイン比熱とデバイ比熱のシミュレーション 
//------------------------------------------------------------------------//
clear;
ET = 300;//アインシュタイン温度
DT = 300;//デバイ温度
kB = 1;//ボルツマン定数。１としておきます。
N0 = 1;//アボガドロ数。１としておきます

temp = [1:1000]';//温度の設定
EinC = 3*N0*kB*((ET./temp).^2).*exp(ET./temp)./(exp(ET./temp)-1).^2;
DebC = 9*N0*kB*((temp./DT).^3).*integrate('x.^4*exp(x)/(exp(x)-1).^2','x',0,DT./temp);

//------------------------ 図の描画とデータ保存 ------------------------//
clf();//表示している図のクリア
plot2d(temp,EinC,2)//アインシュタイン比熱のプロット
plot2d(temp,DebC,5)//デバイ比熱のプロット
legend(['Einstein model';'Debye model'],5)//凡例
xtitle('Specific heat simulation','Temperature (K)','Cv/NAkB');//タイトル

//下記の項目を有効にすると計算結果を保存します。
//TvC=[temp, EinC, DebC];
//savematfile SpecificHeatCalc.txt TvC -ascii -double

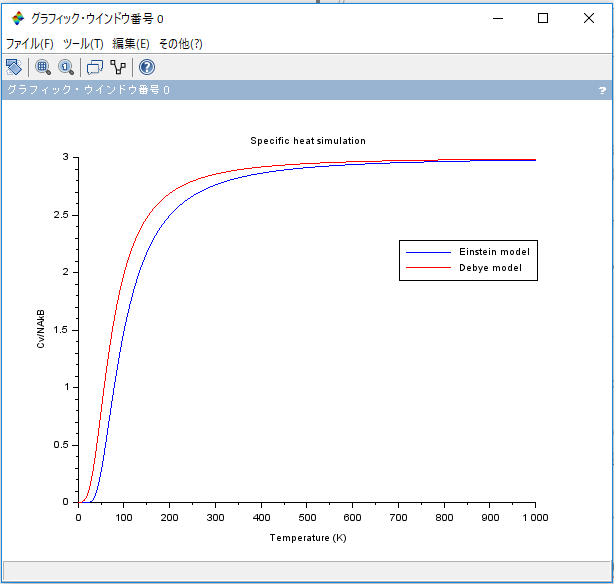
うまくいけば，下図の様なグラフが表示されるはずです。デバイ比熱の計算で出てくる積分についてもベクトル的に（ループなしで）計算できるのに昔驚いた記憶があります。